Article 8:
Gravitational Red Shift and the Speed of the Fast Solar Wind
This is a supplementary article. To go to the main introductory article about Stationary Energy Theory, and its links to other supplementary articles, please click here.
If you refer back to Figures 5 and 6 in Article 6, “How Backward-Through-Time Particles Explain Gravity, Inertia and Angular Momentum,” and the accompanying explanations about how Stationary Energy Theory says gravity works, you will recall that a “backward through time particle” (BTTP), that would otherwise be on a straight-on collision course with a “basic particle” (BP) within an object, is slightly deflected by the presence of other matter nearby in a direction away from that other matter, which creates a repulsive force pushing this piece of matter toward the other matter, which is the attractive force of gravity.
It follows from this deflection of BTTPs that if the two particles are to collide in a gravitational field then the BTTP would be, after its deflection, arriving at the collision at a slight angle to the direction in which the piece of matter is moving forward through time. Since the deflection of the BTTP is proportional to the mass of the other nearby matter, and inversely proportional to its distance, the larger the gravitational field the piece of matter is in, the larger the angle of approach of the BTTP will be at the point of collision.
When this non-straight-on collision occurs, though, the net velocity of the particles after colliding cannot be zero, as is required for them to become EMR in the Universal Energy Field. What could happen, though, and this theory predicts does happen, is that some of the particles remain as matter and carry away the net kinetic energy, and others effectively collide head on and become a part of the Universal Energy Field.
Let’s consider a case where a collision, when straight on, would involve 100
BPs directly colliding with 100 BTTPs, producing a photon of EMR with energy
Es. If the collision were at a slight angle, such that one percent of the total
energy needed to be carried off as kinetic energy, then one BP and one BTTP
could carry off this energy as kinetic energy, leaving 99 BPs to
collide head on with 99 BTTPs and make the quantum jump to the Energy Field.
The quantum of EMR produced would then have 99/100 as much energy as
Es. Its energy, Ea, would be: Ea = 0.99Es. Since the energy carried by EMR is
proportional to its frequency, fa = 0.99fs. In other
words, in this gravitational field, there would be a 1% red shift in
radiation emitted, and this 1% of lost energy would be carried away by the particles
as kinetic energy, half in our Universe by the piece of matter containing the
BP and half by the BTTP in the backward through time domain it
occupies. This can be illustrated as follows, where the deflection angle α is the same angle as α in this theory's basic equation for gravity:

The reverse situation, with the same red shift result, occurs when photons are absorbed (creating absorption spectra lines) in a gravitational field. Since the BTTPs and the BPs matter that are created need to end up traveling in exactly opposite directions through time to satisfy the conservation of momentum, but the gravity of the sun will deflect the BTTP, the particles have to launch off at an angle to each other rather than in directly opposite directions. This is achieved with the help of an incoming particle (perhaps attracted by the gravitational field) which imparts the required KE and mass to the particles (say 1%), so a photon of only 99% the energy normally required need be absorbed. This creates a red-shifted absorption line in the spectrum.
Note from Figure 9 that the velocity of the piece of matter carrying away the KE, when a red-shifted photon is created, is always away from the center of mass causing the gravitational field, rather than toward it, though it may or may not be directly away from it, depending on exactly where the collision takes place with respect to the mass causing the gravitational field. It is also clear that these pieces of matter could be carrying substantial amounts of kinetic energy (KE), as they could be traveling at very high speeds. If the piece of matter consists of just the “basic particle” that carried away this energy, then it would be traveling at the speed of light, and have kinetic energy E = ½mbc².
If a piece of matter, such as a proton, collides with a backward through time particle of the same mass at the surface of the sun, producing slightly red-shifted photons of light and other EMR, then the net energy lost in the red-shift is carried off as kinetic energy by another nearby particle, most likely to be the same type of particle, in this case a proton. Since the red shift at the surface of the Sun is Z = 2.12239 x 10-6, and energy is proportional to frequency, then the total energy lost as kinetic energy in the forward through time domain is Z x ½mc2. Since it is carried away by a particle close to the same mass as the one brought to rest by the collision, and its energy is Z times as high, it will be traveling much more slowly, and its speed can be calculated by equating the energies:
½mwv2 = Z x ½mcc2
where mc = the mass of the colliding particle(s) and mw is the mass of the solar wind particle. So,
v2 = Zc2mc/mw
or for our sun, using velocities in km/sec:
For the case where one proton collides with a similar BTTP, and the red-shift energy loss is carried away as one proton in the solar wind, (mc/mw)½ = 1 and v = 437 km/s.
For the case where two protons collide with similar BTTPs, and the red-shift energy loss is carried away as one proton in the solar wind, v = 436.74972 x 2½ = 618 km/s.
For the case where three protons collide with similar BTTPs, and the red-shift energy loss is carried away as one proton in the solar wind, v = 436.74972 x 3½ = 756 km/s.
For the case where four protons collide with similar BTTPs, and the red-shift energy loss is carried away as one proton in the solar wind, v = 436.74972 x 4½ = 873 km/s.
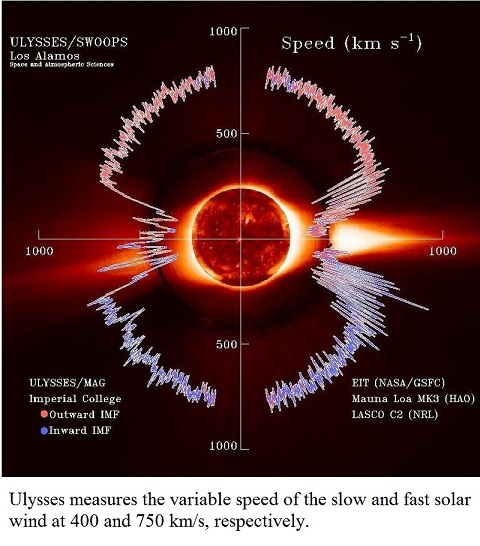
One would expect the measured speeds of solar wind particles to vary somewhat from these speeds due to gravitational slowing and electrical field acceleration. Overall, though, these speeds correspond well to the speeds of the solar wind observed by the Ullyses space craft, as shown in the diagram below. The one particle collision solar wind speed of 437 km/s is typical of the speed of the slow solar wind, which you can see from the diagram varies from just below 400 km/s to almost 500 km /sec. The two particle collision solar wind speed of 618 km/s is significant, as this is also the escape velocity of the sun, so it represents the lower speed limit of the fast solar wind. The three and four particle collision solar wind speeds of 756 km/sec and 873 km/s are typical of the speeds of the fast solar wind. And the average of the two, three and four particle collision solar wind speeds of 749 km/s is right on the fast solar wind average of 750 km/s. As you can see, this theory explains why the solar wind speeds are grouped into specific ranges, rather than spreading across a continuous spectrum of speeds. This theory predicts that the speed of the stellar winds of other stars, should they ever come to be measurable, will be able to be calculated from the above formulas, as we have done for our sun.
These figures, above, would suggest that an average of about one part of matter is lost to the sun due to the fast solar wind for each three parts of matter converted to solar energy by the fusion process, as the average fast solar wind speed of 750 km/s corresponds with one particle of matter carrying away kinetic energy as solar wind for each three particles being converted to energy. This is in line with the figures astronomers give us for the rate of conversion of solar matter to energy of 4.26 x 109 kg/s and the loss of matter from the sun due to solar wind of 1.3 x 109 kg/s to 1.9 x 109 kg/s. This is a ratio of between 1 to 2.2 and 1 to 3.3, right in line with the approximate 1 to 3 ratio this theory predicts.
One of the problems we have had up to now with our theories
about solar wind is that it is not understood how the fast solar wind can
accelerate up to the speeds it does. As we can see from the above calculations,
though, the carrying away of excess energy from the gravitational red shift of
the sun (even though the red shift itself is too small to be easily observed), could
certainly account for the levels of kinetic energy of the fast solar wind.
Stars with much higher gravitational fields than our sun (which are much more massive
and/or denser), could also, in the same way, produce Cosmic Rays, which, like
the solar wind, are mostly protons and electrons, but are much faster than the solar wind,
nudging the speed of light.
Many observations have confirmed Einstein’s famous prediction that photons of starlight passing very close to the sun’s surface will be deflected from their course by the sun’s gravity by an angle of 1.7511” of arc. Stationary Energy Theory suggests that BTTP’s heading toward photon-producing collisions with matter on the photosphere of the sun would be similarly deflected (see Appendix C). However, BTTPs at their point of collision with BPs on the sun’s photosphere will only have been deflected by half the total amount that photons passing the sun are because they are only traveling to a central point on the photosphere and not also away from it like photons of starlight are.
So, knowing this angle of approach of BTTPs to the collision, the net kinetic energy (KE) left over after the collision, as a fraction of the total KE of particles before the collision, can be calculated. As we saw a little earlier, this causes the photon(s) emitted to have less energy, and hence a lower frequency, by the same amount. If both the BTTPs and the BPs they are colliding with were deflected by an angle “α”, the fraction of energy lost as red shift would be Z = sin α, but since only the BTTPs are deflected by this angle, the fraction of energy lost is, as you will see if you refer back to Figure 9:
Z = sin(½α) . . . . . . . (18)
Since BTTPs at the photosphere are deflected by half the angle that light is deflected by when passing the photosphere of the sun (as previously discussed), α = 1.7511/2” = 0.87555”, and
Zs = sin(2.12239 x 10-6) = 2.12239 x 10-6 . . . . (19)
This value for the gravitational red shift of the sun of Zs = 2.12239 x 10-6 is in agreement to six significant figures with the value of Zs = 2.1223949 x 10-6 obtained from the equations of general relativity, which have been experimentally confirmed in various ways. This result is as close as could be expected considering the precision of the value of α used to calculate it, and is a confirmation that the line of reasoning presented here is correct, and BTTPs and photons are, in fact, deflected by the same amount in the presence of bodies of matter.
The rate of conversion of solar matter to energy is about: 4.26 x 109 kg/s. This energy is produced in the core of the sun, but gradually percolates to the surface, where it is radiated at the photosphere. The question is whether the energy lost in the red shift of this radiation is sufficient to account for the mass and kinetic energy of the fast solar wind.
In determining this we will simplify the calculation by looking at just the BPs in matter, and only consider the half of the KE carried away by particles of matter, though an equal mass of BTTPs are involved, and an equal amount of KE is carried away by them.
With this rate of conversion of matter to enegry, the amount of energy lost by the sun’s gravitational red shift, measured by its mass, is:
Energy lost = Zs x 4.26 x 109 kg/s = 2.12239 x 10-6 x 4.26 x 109 kg/s = 9.04 x 103 kg/s
This 9.04 x 103 kg/s is the amount of matter that would carry away half the lost energy as KE if it were traveling at the speed of light, “c” (the other half is carried off by BTTPs). This amount of KE could also be carried away by about 160,000 (close to 1/(3Z)) times as much matter if its speed were 750 km/s, a typical speed for the fast solar wind. This would give a total possible rate of emission of fast solar wind (SWf) of:
SWf = 9.04 x 103 x 160,000 kg/s = 9.03 x 103 x 1.6 x 105 kg/s = 1.45 x 109 kg/s
This rate of emission of 1.45 x 109 kg/s is right in the range of the estimated loss of matter from the sun due to the solar wind, which is about 1.3 x 109 kg/s to 1.9 x 109 kg/s. This is based on the assumption that the solar wind starts at the photosphere at a speed of 750 km/s. If the fast solar wind starts off at a much higher speed and is slowed down the sun's gravity more than it is sped up by magnetic fields, then this mechanism might only cause the fast solar wind, and not also the slow. There are, of course, other mechanisms that can explain the slow solar wind. It is clear, though, from the above calculations, that all of the fast solar wind, at least, can be produced by energy lost from the sun’s gravitational red shift. This gravitational red shift explanation of the production of the fast solar wind has the particles of the fast solar wind originating at the photosphere. As a result, one would expect, from this theory, that the elemental composition of the the fast solar wind should resemble that of the photosphere. It is interesting to note that observational data indeed shows this to be the case. The fact that the slow solar wind has a different elemental composition suggests that it is not all produced by this gravitational red shift mechanism.
Being of substantial mass, though much less than the sun, the Earth, too, should produce a gravitational red shift in electromagnetic radiation produced by sources such as light bulbs and hotplates on stoves. And if the Stationary Energy Theory is correct in saying that the fast solar wind is powered by energy lost in the gravitational red shift on the sun, then the same thing should occur on Earth, though to a much smaller degree. EMR sources such as an electric stove hotplate should emit particles of matter in a direction approximately away from the center of the Earth at a sufficient speed to carry away as kinetic energy the energy lost in the gravitation red shift of the EMR produced. It is a prediction of the Stationary Energy Theory that these particles should be emitted, and it is quite possible that an experiment could be devised to detect them. To lay the groundwork for such an experiment, let's do some math to determine the likely quantity and speed of such particles when coming from a source on Earth.
First let's work out the gravitational redshift on the Earth's surface, using Equation 18, derived earlier in this article, Z = sin(½α). For the small angles involved this becomes
Z = 0.5×5.972×1024 × 1.485143333754 × 10-27/6,378,000 = 6.953 × 10-10
So, Z for the Earth is about 3,000 times smaller than Z for the sun. We'll assume for the moment that the average ratio of the mass converted to energy to the mass of particles carried away is equal to 3 for the Earth, just as we saw earlier in this article that it is for the sun. The very different energy producing environments on the sun and Earth could, of course mean this ratio is different on the Earth, but it is a good place to start to get a ballpark figure for how fast these particles might be traveling. We can then use Equation 17, derived earlier in this Article, to calculate the average speed of "Earth wind" particles. This equation is: v = cZ½(mc/mw)½.
v = 299,792,458×(6.953 × 10-10)½×3½ = 13,690 m/s.
This is about 50 times slower than the fast solar wind, but it is still very fast: above the escape velocity of Earth, and about 30 times greater than the speed of gas molecules in our atmosphere. This should make detecting them quite possible if there are a sufficient number of them being emitted. So let's move on to calculate the total mass of these particles that should be being emitted. First we will calculate the total energy, in Joules, emitted, by a 1000 W electric stove hotplate in 1000 hours of use. This total energy is the number of Watts times the number of seconds:
E = 1000×3600×1000 = 3.6 ×109 Joules
The amount matter converted to energy to get this amount of energy, according to the equation E = mc², is m = E/c², which is:
3.6 ×109/(299,792,458)² = 4.0 × 10-8 kg or 0.040 mg (milligrams).
Since our 'ballpark' ratio of converted matter to emitted matter is equal to 3, this means only about one third of this amount, or about 0.013 mg of particles per 1000 hours are being emitted as "Earth wind." This is just 3.7 × 10-9 mg of particles of "Earth wind" per second. This is a tiny quantity, but it is still a substantial number of particles. If the particles are electrons, as a good many of them may be, there would be 4.1 × 1015 particles emitted per second. If the particles are tungsten atoms, which many of them may be, too, there would still be over 1010 (ten billion) of them being emitted each second. So although the mass of particles being emitted per second is extremely tiny, the large number of actual particles and their high speed, generally away from the center of the Earth rather than toward it, may well serve to make them detectable in a well designed experiment with sensitive measuring equipment.
Press your browser's "back" button (<) to return where you were in the main article.
To go to the beginning of the main introductory article, please click here.
To go to the next article in the series, Article 9, please click here.
or
v = cZ½(mc/mw)½
v = 299792 x 0.001456842476 x (mc/mw)½
or
v = 436.74972 x (mc/mw)½
This theory predicts a value for the gravitational red shift of the sun at its photosphere, and from this a general formula for gravitational red shift can be derived
½α = 0.437775” = (0.437775/(60×60))π/180 = 2.12239 x 10-6 radians, so:
Is there enough energy lost from the sun’s gravitational red shift to produce the solar wind?
The Earth's Equivalent of the Solar Wind - The Earth Wind
Z = ½α. α is the deflection angle already referred to in this article, which is equal to half the gravitational lensing of light due to a massive object. We will use Equation 30 derived in Article 15, α = m1 × 1.485143333754 × 10-27/d, to calculate α for the Earth, and Z will be half of that, so:
Using mc/mw = 3 (our assumption above) we get: