Article 7:
How Gravitational Attraction Becomes a Repulsion at Great Distances

This is a supplementary article, and will not make much sense if you haven't already read the Main Introductory Article and the preceding supplimentary articles. To go to the Main Introductory Article about Stationary Energy Theory, and its links to other supplementary articles, please click here.

It was mentioned in the introductory article that the inverse square law attraction of gravity may not apply in all situations in the Universe. One situation where this theory suggests it should break down is over very large distances that are a significant fraction of the radius of the Universe.

Looking at Figures 5 and 6 again (in Article 6), the presence of m2 repels p1 slightly so that it passes m1 on the side away from m2, causing p1 to repel m1 and push it toward m2, creating (one half of) the attractive gravitational force between m1 and m2. As the distance between m1 and m2 increases, the angle of deflection of p1 is going to reduce, until at very great distances it will be very tiny. At small distances the directions of movement of m1 and m2 are effectively parallel, but at very great distances, that are a significant fraction of the radius of the Universe, the direction of movement of m1 and m2 will cease being parallel, due to the curvature of the three dimensional “surface” of our four dimensional spherical Universe. Instead they will “splay” outward. When this angle of splay becomes larger than the tiny deflection caused by m2, p1 will repel and be repelled by m1, and pass m1 on the side toward m2, and continue to repel it away from m2. Thus, at these huge distances, gravity should, according to the Universal Field Theory of Cosmology, become a repulsive force, rather than an attractive force. In this situation, “I” in Equation 15 (F = IGm₁m₂/d², from Article 6), becomes negative. In general, Stationary Energy Theory says the force of gravity is described by Equation 15, where I is not always equal to one, but reduces in value, then turns negative, at great distances. Figure 7, below, illustrates this situation where gravitation becomes a repulsive force.

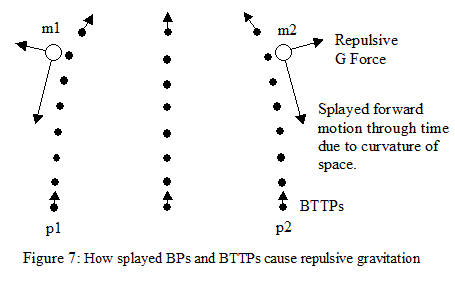
For tiny pieces of matter, such as hydrogen molecules, isolated from other gravitational fields (or in orbit or free fall), the deflection of p1 by m2 would be extremely tiny, even at relatively short distances. This could mean that the “splay” in the direction of movement of the hydrogen atoms could become greater than the repulsive deflection of the BTTPs when they are only a tiny fraction of a meter apart, causing the gravitational force between them to become one of repulsion, rather than attraction, when they are further apart than this critical distance. This is the other situation where this theory suggests the inverse square law attraction of gravity should break down, and “I” (in Equation 15) would become less than one then turn negative. This would help explain why there are still large numbers of isolated atoms and molecules of matter floating around in space, especially intergalactic space, that haven’t been attracted to each other to form stars. (This gravitational repulsion of tiny particles at quite small distances will be further discussed in Article 14.)

These two situations where gravity is a repulsive force would also explain why gravity isn’t slowing down the expansion of the Universe, as one would otherwise expect it to do. The evidence is that the speed of expansion of the Universe is currently actually increasing. Gravity turning into a repulsive force at very great distances, and at even quite small distances for very tiny particles, as this theory suggests, could certainly explain the accelerating expansion of the Universe, and do so much more elegantly than by proposing the existence of vast quantities of undetected “dark energy” that repels matter and itself rather than attracting it. Once we have derived a formula for the force of this repulsive gravity in Article 15, we will show, in Article 16, that it can also fairly accurately account for the observed rate of acceleration of the expansion of the Universe.

One could, if one wished to, say that the BTTPs are the “dark energy.” They certainly have the required quality of dark energy of repelling matter. The function of BTTPs, though, goes far beyond that proposed for dark energy, so I believe it would be confusing and misleading to equate them in any more than a superficial way.

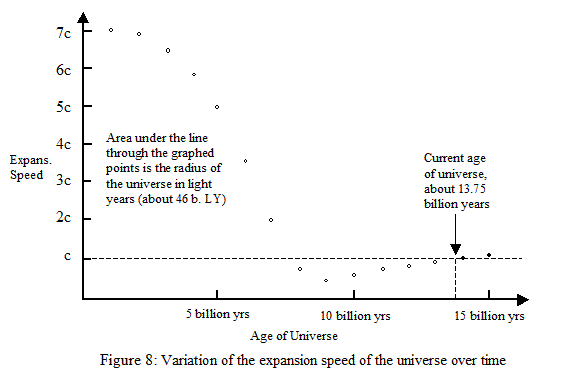
We should note here that the expansion of the Universe has not always been accelerating. For the radius of the Universe to be over three times greater in light years than its age in years, the Universe must have had an average speed of expansion over its lifetime of over three times its current speed. The evidence suggests that the Universe has been expanding for about the last five billion years, just over one third of its age. This means that the speed of expansion of the Universe must have started off, after the big bang, many times faster than it now is, and have slowed down for about nine billion years, after which its speed of expansion began to increase again.

The current five billion year long acceleration of the speed of expansion could be the first major return oscillation after an initial nine billion year slow down. Figure 8, below, illustrates this.

Press your browser's "back" button (<) to return to where you were in the main article.

To go to the beginning of the main introductory article, please click here.

To go to the next article in the series, Article 8, please click here.