Article 4:
Structure of the Universe According to Stationary Energy Theory

This is a supplementary article. To go to the main introductory article about Stationary Energy Theory, and its links to other supplementary articles, please click here.

Stationary Energy Theory proposes that the matter of the Universe is always traveling at the speed of light with respect to the electromagnetic energy of the Universe. This electromagnetic energy is seen as being always stationary with respect to a frame of reference centered on the Big Bang event. I call this energy the “Universal Energy Field.” When the speeds of material objects through space are slow, most of their speed-of-light movement is through a fourth, time, dimension, which is perpendicular to the three space dimensions. This movement through the time dimension gives rise to our perception of time passing.

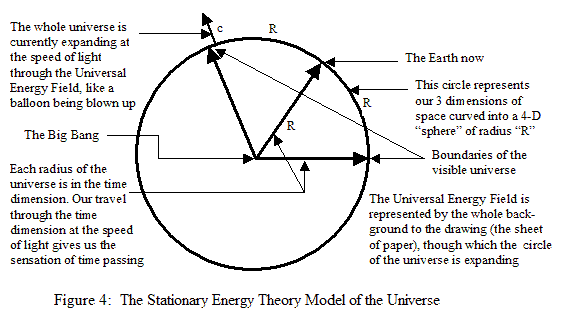
If this Universe started at a point, or was once very small, this movement of matter along the time dimension would have to be in a direction outward from the center, and would produce a Universe in the form of, or very close to that of, a four dimensional sphere, expanding at the speed of light, or very close to it, along all possible radii of the sphere, from the center to the “surface.” The “surface” of this sphere is our three dimensional Universe, which is also expanding. The rate of this expansion is linked to the radial expansion, so that two points on this sphere one radian (one radius distance) apart will be moving away from each other at the speed of light. It is expanding like the surface of balloon expands when it is being blown up. As a result, this theory is in accord with the observations of astronomy that show that the most distant observable galaxies are moving away from us at almost the speed of light.

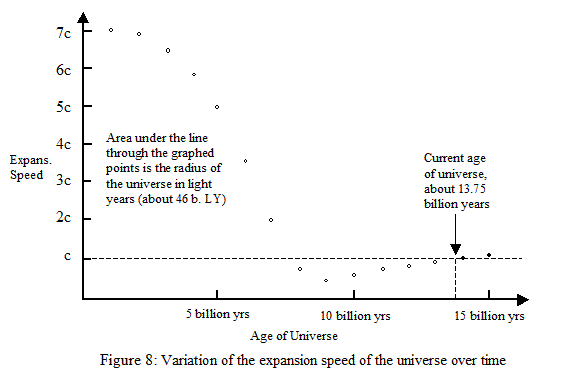
If the speed of light has always been the same, since the Big Bang, this theory requires the radius of the Universe in light years to be equal to the age of the Universe in years, which runs counter to current astronomical observations that suggest the radius of the Universe in light years is over three times its age in years.

This theory, however, does not require that the speed of light has always been the same — it just says that, because the apparent speed of light is due to matter expanding through the “stationary” Universal Energy Field of the Universe, the speed of light at a given point in time is equal to the speed of the expansion of the Universe at that time. So, rather than requiring an equal age and radius, this theory suggests that if the radius is larger in (our current) light years than its age in years, it is because the speed of the expansion of the Universe, and the speed of light, were greater in the past than they are now.

And it is not unreasonable to suppose that the speed of expansion of the Universe would have been greater just after the Big Bang, and that it subsequently slowed down to its current speed or a little below. The following diagram illustrates how this might have happened:

It is important to note that although Stationary Energy Theory says the speed of light may change over long periods of time as the speed of the expansion of the universe changes, we will, nevertheless, always measure the speed of light as being the same. This is because, under this theory, our rate of travel through time (when close to being at rest in space) is equal to the speed of light. Let's say the speed of light increases by 10%. Since speed is distance/time, the distance traveled in the old time is 10% higher, but our speed of travel through time increases, too, by the same amount, so 10% more seconds will pass compared to the old speed of time. These two 10% increases will cancel each other out leaving us measuring the speed of light at the same speed we always did, even though from a large-scale, four-dimensional viewpoint its speed has changed. This is a little bit like us not being able, even in theory, to directly measure the 'metric' expansion of the universe over time, because whatever measuring rod we use will have expanded, too, since the very fabric of space, including the matter in it, expands everywhere. To picture this, think of the polka-dot-balloon model of the universe described in the Introductory Article. It has a little ruler drawn on it, and as the balloon is blown up, not only do the polka dots expand and move away from each other, but the ruler also gets bigger so that using this ruler to measure the size of the balloon will always show it to be the same size! From outside the two-dimensional balloon surface, though, looking at the balloon in three dimensions, we can see the balloon is in fact getting larger as it is blown up.

While no point on a sphere is special compared to any other point, it is possible to specify a grid showing how each point is related to every other point, in terms of angles subtended to the center of the sphere. We do this with latitude and longitude on the Earth.

If you start with any one radius line, going from the center of the sphere to the surface, then the point at which this radius line intersects with the surface can be specified as a “stationary point” on the surface of the sphere, and a grid can be constructed, in terms of angles from a line drawn through this point, and angles subtended from the center of the sphere from this point.

Any other point on this grid is then also a “stationary point” where another radius from the center of the sphere intersects with the surface. If a train or a ship is traveling along the surface of this sphere, one can specify its speed relative to the point on the ground directly below it, which is a fixed point on the latitude and longitude grid. Each point on the grid is a “stationary point,” and it is valid to talk about how fast an object is moving with respect to that point. And this would still be true if the Earth were a gradually expanding sphere. If the sphere is expanding, though, each “stationary point” (grid point) will be moving away from every other “stationary point,” as these points are only “fixed” in relation to each other in an angular way.

The Stationary Energy Theory model of the Universe is analogous to such a gradually expanding Earth, and has to be for the Universe to be isotropic. Any point at which an object’s (or observer’s) passage through time intersects with the “surface” of the four dimensional sphere of our Universe (the current moment for that observer) is a “stationary point” the object’s speed can be measured against. These lines along which time passes are, by definition, radius lines of the Universe, that originate at its center and intersect the four-dimensional sphere perpendicular to all three space dimensions at every such “stationary point”. And, as we established in Supplementary Article 2, in order for the Universe to be isotropic, these lines along which time passes must intersect our three dimensions of space at a “single point.” Not only can the speed of an object be measured with respect to such a “stationary point” as we have described (which if it were on the Earth would be the point “directly below it”), but, it is also a consequence of this model of the Universe that the speed, “v”, used to calculate how much time is slowed down for a moving object (to keep the speed of light always constant), is the speed relative to such a “stationary point.” These “stationary points” are the “points in space” we referred to earlier.

Article 13, “Stucture of the Universe - Local Flattenings - dimples on a golf ball” elaborates on this basic structure, presented here, to explain how superclusters of galaxies occupy areas of local flattening of the overall spherical universe, and to show how these areas of local flattening arise and affect gravitational forces.

To return to where you were in the main article, press your browser's "back" button (<)

To go to the main introductory article on Stationary Energy Theory, please click here.

To go to the next article in the series, Article 5, please click here.