Article 13:
Structure of the Universe -- Local Flattenings on a 4D Sphere

This is a supplementary article. To go to the main introductory article about Stationary Energy Theory, and its links to other supplementary articles, please click here.

This theory predicts local flattenings of the curvature of the spherical universe which contain galaxy supercluster complexes

Within our part of our galaxy (LS), we know there is a general movement of stars of about 630 km/s with respect to the Cosmic Microwave Background Radiation (CMB) rest frame. I have already hinted that the CMB rest frame and the grid of “stationary points” of this theory are one and the same thing, and I will formally propose it in a later article in this collection of articles. According to Stationary Energy Theory, this movement with respect to the rest frame means that there should be a certain small amount of reduction in the rate of passing of time, as a result of this movement, compared with other parts of the Universe that are at rest with respect to their “stationary points.” Since the Universe is expanding in the time dimension, if the rate of passing of time is reduced in a particular area of the Universe, in this way, then one would also expect that that area would have expanded less than the areas around it, and that its outward curve would be flattened somewhat, at least, and perhaps be largely or completely flattened or even be reduced to a concavity.

Let’s assume for the moment that we are a part of a local area where the Universe has been totally flattened out so that it has no curvature. The center of such an area would be where the speed is the greatest and the edges would be where it is the least. Let's assume we are half way out from the center of such an area, and we are moving at half the speed that the center is. We can then calculate how big this area of flattening is, based on the current estimate that our galaxy is moving at a speed of 627 km/s with respect to the rest frame. At the center of this flattened area, the speed would be twice our speed, or 1254 km/s. At this speed, this center's rate of passage through time compared with the rate of passage through time of a place at rest, “T₀”, is given by Equation 6 (from Article 2):

T = T₀(1 - v²/c²)^½

Plugging in the values of v = 1254 km/s, and c = 299,792 km/s, we get:

T = T₀(1 – 1254²/299,800²)^½ = T₀(1 – 1,572,516/89,880,040,000)^½

   = T₀(1 – 1.749571985 x 10^-5)^½ = T₀(0.99998250)^½ = T₀ x 0.999991252, so:

T = 0.999991252T₀

If this local slightly smaller rate of the expansion of the Universe has been the same since the Big Bang, then the current radius of the Universe at this point will be smaller than the general radius by the same amount, so:

R = 0.999991252R₀           .            .            .            .            .            .            .      (26)

Let’s see what this looks like on a diagram:

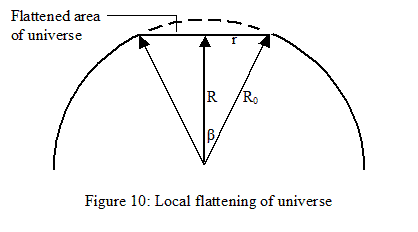
From (26) above and Figure 10:

R/R₀ = 0.999991252 and R/R₀ = cos β, so:

β = acos 0.999991252 = 0.004182906 radians (about 0.24°).

Also, r/R₀ = sin β, so:

r = R₀ x sin β    .           .           .           .           .           .           .           .           (27)

Now “r” is the radius of the flat spot around our galaxy that we are looking for, R₀ = 46 billion light years — the radius of the Universe, and we just found the value of β, so:

r = 4.6 x 10¹⁰ ly x sin(0.004182906) = 1.924 x 10⁸ light years.

This gives a diameter (twice the radius found above) for our local “flat spot” of 384 million light years, about 400 million light years in round figures, significantly larger than our Local Supercluster, as it would need to be, the diameter of which is variously estimated to be from 110 to 150 million light years.

This explains why the geometry of space has been observed to be "flat" (to within one part in 200) in our part of the universe, but is spherical overall as it must be if the universe's expansion has been from a single point at the Big Bang.

The splay between adjacent “flat spots” on the four dimensional sphere of our Universe will be the same as the splay between the points on a sphere at the centers of the “flat spots”, since the centers of the flat spots are parallel to a tangent to the sphere. This splay will then be the splay between any point on one flat spot and any point on the other flat spot. Since flat spots seem to have a radius of about 200 million light years, their centers must be at least 400 million light years apart, and probably quite a bit more, perhaps 800 million to 1.6 billion light years, to take account of the voids between them where the Universe is curved. So let’s work out what the critical distance of two superclusters would be, with f = 1. The mass of our local Supercluster Complex is estimated to be: 1 x 10¹⁸ times the sun. The critical distance, from Equation 24 (derived in Article 12) is then:

dc = 0.16946 x (1 x10¹⁸ x 1)^½ = 1.6946 x 10⁸ ly

This critical distance of “flat spots” containing superclusters of about 170 million light years is way below their distance apart of at about 800 million light years, so these “superclusters complexes” (on separate “flat spots”) are certainly going to be repelling each other, and it is this repulsion, according to this theory, that is keeping the Universe expanding, and driving the current acceleration of its expansion.

Within the Local Supercluster Complex, if the flatness is f = 2,500 (which we earlier estimated to be a reasonable flatness based on the apparent slight attraction between our galaxy and the Andromeda Galaxy and other factors) then the critical distance of the LS would be 2,500^½ = 50 times greater, or 8.5 billion ly, well over the estimated width of the complex of one billion ly, so more than enough to account for its cohesion. This seems to confirm that f = 2,500 is a pretty good estimate of the flatness of the “flat spot” that contains our Local Supercluster.

To make up for the lack of curvature in the flat spots, and maintain an average curvature of f = 1, the curvature of areas between the flat spots must be about twice the average (f = 0.5). With this curvature, the critical distance of two galaxies the size of the Milky Way would, from Equation 24, be: dc = 0.16946 x (1 x10¹² x 0.5)^½ = 120,000 ly, and any galaxies further apart than this would repel each other rather than atract each other. As a result of galaxies nearly all repelling each other inbetween flat spots, this theory suggests that over time nearly all galaxies would move out of these regions into adjacent flat spots, leaving them largely empty. This nicely explains why there are voids between complexes of superclusters of galaxies.

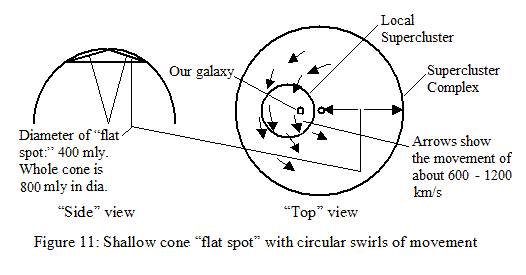
I would like to suggest that the “flat spots” in the Universe may not just be four dimensional analogs of “disks,” but may be 4-D analogs of shallow cones. This would enable the movement to go around in large circles, or “swirls,” rather than actually going somewhere in the wider Universe. Since on every level of the Universe we see matter orbiting around in circles or ellipses, it would hardly be surprising if this were also to happen on the level of the movement of galaxies with respect to the CMB rest frame. These “flat spot swirls” could, as Figure 11, below, shows, average about 800 million light years in diameter.

As can be seen from the above discussion and calculations, this theory predicts that the local geometry of the Universe, within supercluster complexes is “flat” to within about one part in 2,500 (the value of the “flatness factor”, “f”), but that the global geometry is “spherical” with little flat patches all over it — kind of like a golf ball if you filled its dimples in until they were flat. This agrees with the recent astronomical observations that suggest the local geometry of the Universe is flat to within ±0.5% (one part in 200). The Poincaré dodecahedral space, a model that apparently fits the data, is the closest prior model. This theory, however, predicts that the global geometry is that of a polyhedron with hundreds of thousands of “flat spots,” each probably about a degree across, or two degrees if they are “swirls.”

Not only does this theory explain why the local geometry of the universe is "flat" within the overall context of a spherical universe, but it also explains why galaxies are collected into superclusters of galaxies separated by voids: superclusters occupy the flat spots and the voids are the more curved regions between the flat spots. Negative gravity operating at much smaller distances in the curved areas between flat spots would have caused most matter to be expelled out of these areas into surrounding flat spots, which explains why these areas are voids.

If it doesn’t seem like hundreds of thousands of 2° “flat spots swirls” in their surrounding voids could fit on a sphere, bear in mind that we are talking about a 4-D sphere here. The “bounding volume” of a 4-D sphere is given by S₃ = 2π²R³. Using this formula it turns out that this bounding volume could contain 464,095 2°-width cubes, each of which could be home to a “flat-spot swirl”. Assuming each of the 464,095 “flat spot swirls” contains an average of a Local Supercluster Complex’s worth of mass, the mass of the Universe would be about 4.6 × 10²³ suns, or 9.2 ×10⁵³ Kg. Interesting, considering we calculated earlier that the mass of a “basic particle” is probably about 10^-53 kg. It seems like the macro and the micro in the Universe might be fairly evenly balanced.

Since a hydrogen atom weighs about 1.67 ×10^-27 Kg, this theory suggests there would be about 9.2 ×10⁵³/1.67 ×10^-27 = 5.5 ×10⁸⁰ hydrogen atoms in the universe, if all the atoms were hydrogen. There are other heavier atoms, too, so we could say there would be about 5.0 ×10⁸⁰ atoms in the universe. Since our visible universe is only about 20% of the whole universe, this means there should be about 10⁸⁰ atoms in our visible universe.

Press your browser's "back" button (<) to return to where you were in the main article.

To go to the beginning of the main introductory article, please click here.

To go to the next article in the series, Article 14, please click here.