The Magical Math of the Universe
Or Why God Loves Simple Math
Author: Mark Mason
It has been said that ‘mathematics is the queen and servant of science.’ Sometimes this math that explains the universe can be very complicated, but at other times it can be very simple and elegant, to an extent that is breathtaking and seems almost magical. It can also, at times, be simple enough that an average ninth grade math student could easily understand it. This is the sort of math I’ll be presenting here, explaining everything so you won’t even have to remember your ninth grade math!
The ‘Square on the Hippopotamus…
The ‘hippopotamus?’ Well, actually I meant the ‘hypotenuse,’ but thinking of it as a hippopotamus might help you remember it. The hypotenuse is the longest side of a right-angle triangle, and is always the side opposite the right angle. In case you don’t know, a right angle is the angle between two adjoining sides of a square or something that is square. Walls of houses are generally at right angles to each other, as are lots of other things, in order to look like they are not crooked, so it’s a pretty useful concept. I guess in building it’s the ‘right’ angle as distinct from the ‘wrong’ angle. Here is a right angle triangle with the hypotenuse marked:
Right angled triangles have a special property that mathematicians from most ancient civilizations, including the Babylonians, Mesopotamians, Indians, Chinese and the Greeks were all aware of. It’s this: the square sitting on the hypotenuse has the same area as the areas of the squares on the other two sides added together. Another way of saying this is ‘In a right angled triangle, the square on the hypotenuse equals the sum of the squares on the other two sides.’ This is called Pythagoras’s Theorem. This is what it looks like for a triangle with sides 3 units, 4 units and 5 units. This could be 3 ft, 4 ft and 5 ft, or 3 meters, 4 meters and 5 meters—it’s true for any units you want to use. It’s also true for all right angle triangles, no matter what their size or shape. It’s just that the math works out particularly easily for the 3, 4, 5 triangle, so we will use it for our example:
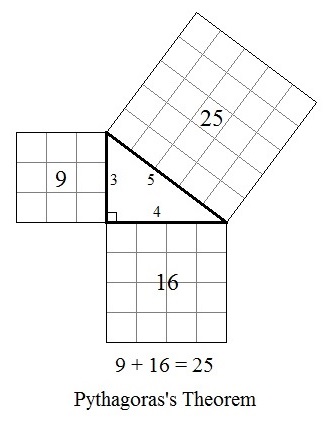
You can count up the squares on the above diagram yourself to check that it really is true: the square on the hypotenuse equals the sum of the squares on the other two sides—it’s kind of magical, because it says something about the nature of the universe we live in. It is also very practical for a number of reasons, one of them being that it makes it easy for us to make buildings and other things very square just by using a tape measure.
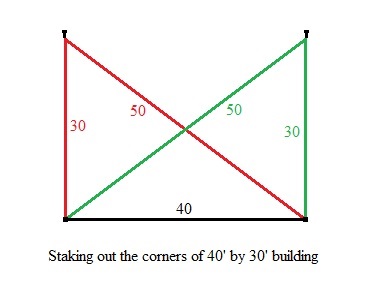
If you are putting the corner posts in for a building of size 40 ft by 30 ft, you could start by putting in one stake where one corner post would be, then measuring 40 ft along where you want the front to be and putting the second stake in. But when putting in the third and fourth stakes, how do you know where to put them so all the angles will be square? With Pythagoras’s Theorem it is easy. Just attach a piece of strong (unstretchy) string to each of the front posts, and measure out 30 ft on one string while it is stretched tight and mark it with a black marker, and 50 ft on the other string and do the same. Where the two strings pulled tight come together at the marks you put on the strings, that is where one of the back stakes go. Switch the strings around and it will give you the place where the other back stake goes. Here is what it looks like, with red and green strings:
Pythagoras’s Theorem is also very useful in adding and subtracting ‘vectors.’ But hold on a moment! What are vectors? Vectors are something very common in the real world—they are things like forces and velocities that have a direction (in fact a velocity is a speed that has a direction). A real world example is a boat sailing along in one direction, say at 4 mph to the east, but which encounters a current of 3 mph going to the north. A vector diagram and Pythagoras’s Theorem can be used to figure which direction the boat actually ends up going, and how fast. Here is a diagram for this example:
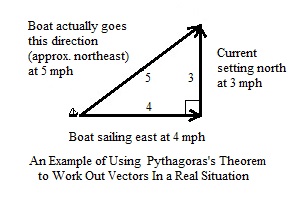
As you can imagine, such diagrams are very useful for captains of boats and ships and pilots of airplanes. They can see little triangles like this inside their heads whenever they are navigating their way through cross winds or currents.
Of course, Pythagoras’s Theorem works for all right angle triangles, not just for 3, 4, 5 ones. In general, Pythagoras’s Theorem is described by this equation:
c² = a² + b² (‘c’ squared = ‘a’ squared plus ‘b’ squared)
where ‘c’ stands for the length of the hypotenuse of a right angle triangle, whatever it may be, and ‘a’ and ‘b’ are the lengths of the other two sides. Don’t be scared by these letters instead of numbers, the superscript ‘2’s and the equal sign in the equation. It’s just saying that whatever value ‘a’ and ‘b’ take, you can work out what ‘c’ is by using this equation. So, with the example we have been using, a = 3 and b = 4 and so:
a² + b² = 3x3 + 4x4 = 9 + 16 = 25
And c² is equal to this, so:
c² = 25 This means c x c = 25, and we know that 5 x 5 = 25 so we have worked out that c = 5 in a right angle triangle when a = 3 and b = 4. The math way of saying this is that 5 ‘squared’ is 25 and the ‘square root’ of 25 is 5. In math notation we would say: 52 = 25 and 25½ = 5.
Another way of indicating the square root is with the square root sign: √25 = 5.
If superscripts are not available, 52 can be written 5^2, and √25 can be written 25^0.5
So for those of you who needed to brush up on it, you now know some algebra again!
We know that Pythagoras’s Theorem works for 3, 4, 5 triangles, and I’ve told you it works for any right angle triangle. But how do we know that? Do we just try it out for lots of different values and see if it works for all of them? Certainly that’s been done, and it does work each time, but this still doesn’t prove it always works for any possible right angle triangle. As we’ve mentioned, mathematicians in most ancient civilizations knew about this property of right angle triangles a long time before Pythagoras was even born. We name the theorem after Pythagoras because he was, as far as we know, the first person to prove, 2,500 years ago, that it works for all right angle triangles. His proof was done by rearranging the triangles inside a square like the left hand square in the following diagram so they looked like the right hand square:
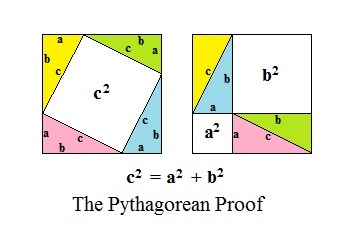
In this proof, we draw the four triangles inside the square by measuring any distance in from one corner (distance ‘a’ in the diagram) and mark it, then measure the same distance in from the remaining three corners and mark them, then draw lines between these four points. The shape of the triangles depends on how far in our marks are from the corner, but each of the triangles is exactly the same size and shape, each is a right angle triangle with the right angle in the square corner, and each has its hypotenuse facing inward. The white uncovered space in the square is a smaller square which is the square on the hypotenuse of each of the triangles. So the white space has an area of c².
This is pretty nifty in itself, but the true magic happens when you move three of the triangles. First, move the blue triangle to the upper left so it is next to the yellow one. Second, move the pink one as far as possible to the right. Third, move the green triangle down so it is next to the pink one. This is the right hand drawing, where you can see there are two white squares, with a total area of a² + b². But since we’ve just rearranged the same triangles in the same large square, the white area remaining must be the same before and after the rearrangement. This means c² = a² + b². And this is how Pythagoras proved his theorem! There are many other more complicated geometric and algebraic proofs of this theorem, but this ‘proof by rearrangement’ remains the simplest and most elegant of all.
Three Magical Facts About the Universe We Live In
We live in a universe made of matter and energy. Matter is the things that are all around us, including our bodies. Energy is what gets things moving. The main form of energy is called electromagnetic radiation, or EMR, examples of which are light, the sun’s heat, X-rays and radio waves.
Magical Fact Number One
When measured by us creatures made of matter (relative to us, as a scientist would say), light and all other types of EMR travel at an immensely fast speed. If you had a car that had done 186,000 miles, it would have taken you 15½ years at 12,000 miles a year to drive all those miles, and along the way your car would have had 62 oil changes. You could have driven right around the world over seven times to go this distance, though you probably didn’t. This is a huge distance, but light travels this distance of 186,000 miles in just one second! In physics, the speed of light is represented by the letter ‘c’.
Magical Fact Number Two
The speeds we measure of other physical things in the universe we live in depends on our own speed. For instance, if we are in a car in the slow lane doing 50 mph, and a car passes us in the fast lane doing 60 mph, we will see it passing us at just 10 mph, but if a car doing 60 mph passes us going the opposite direction, it whizes past us at 110 mph. People expected the measured speed of light to be affected in the same way. So if you are traveling toward a star at half the speed of light you would expect your speed and light’s speed to add together to be 1.5 times the resting speed of light (1.5c). Likewise, you would expect light from a star behind us to only be traveling at half the resting speed of light when it caught up with us (0.5c). A famous nineteenth century experiment, however, the Michelson-Morley Experiment, showed that this is not true, and that the speed of light in a vacuum is always the same (c) regardless of the speed of the light source or the speed of the observer. Many subsequent measurements have confirmed this, and this astounding and highly un-intuitive fact totally changed our view of the universe we live in, and was found to have some very interesting consequences.
Magical Fact Number Three
The most interesting consequence of the constancy of the speed of light in a vacuum has been found to be that time passes more slowly for objects that are traveling close to the speed of light. There is a very famous, and quite magical, equation that describes how time slows down for an object as its speed increases. It is called the ‘Lorentz Transformation for Time Intervals,’ or more popularly, the ‘Time Dilation Equation.’ Although originally derived by Lorentz, Einstein adopted the Lorentz Transformations into his Theory of Special Relativity, and made them famous. The equation looks like this:
t = t0/(1 - v²/c²)½
or using the square root sign:
t = t0/√(1 - v²/c²)
It can also be written:
t = γt0
where γ = 1/√(1 - v²/c²), the ‘Lorentz factor.’
I’ll now explain what all the parts of this equation mean. ‘t’, what we want to know, is how long a particular interval of time, such as a second, lasts for an object or a person when traveling at the speed ‘v’. ‘t0’ is how long the time interval normally lasts for when ‘v’ is zero. ‘/’ is, of course, the divide by sign, and ‘c’ is the speed of light. So let’s plug some figures into this equation, and see how much time would be slowed down if we were traveling at 99/100 (99%) of the speed of light. We will be calculating how many ‘normal speed’ seconds one second would last at this speed. A normal speed second is t0 = 1 second.
The speed of light, c, is very close to 300,000,000 m/s (meters per second).
In scientific notation we can write this as 3 x 108 m/s (‘three times ten to the eighth,’ a ‘3’ with 8 zeros after it).
At 99/100 of the speed of light, v = 2.97 x 108 m/s (put 0.99 x 3 into your calculator)
Now we can work out what ‘t’ is using a calculator. And I encourage you to work it out on your own calculator as you read through the steps!
First v² = 2.97 x 2.97 x 108 x 108 = 8.8209 x 1016
Ta da! The final result: 7.1
So if an astronaut were out there traveling at 99% of the speed of light (which our technology is far from being able to achieve at the moment), each of his seconds would last 7.1 of our seconds. That means that for each 7.1 seconds that passes on Earth, only 1 second would pass for the astronaut, because time is passing over 7 times slower for him than for us. This in turn means that 7.1 years would pass on Earth for every year that passed for astronaut, and 71 years would pass on Earth for ever 10 years that passed for him. If such an astronaut, traveling at this speed were away 20 years, when he got back to Earth 142 years would have passed on Earth, and everyone he knew before he left would be dead. This astronaut would have time traveled 122 years into the future! This may seem quite magical, but it is true! It shows time travel is possible, but only on a one-way trip to the future—there would be no coming back to our time. There can also be no time travel to the past, which protects us against the danger of our time line being altered, such as by someone going back in time and killing one of our parents before we were conceived!
But how do we know this ‘time dilation’ actually happens? We know because we can actually see it happening. There are subatomic particles called Muons that normally only exist for about two one-millionths of a second before decaying to other particles. When accelerated close to the speed of light in a cyclotron, though, these particles can last for close to a full second before decaying, showing that time is greatly slowed down for them, by the amount the time dilation equation predicts.
It can be shown, mathematically, that the time dilation equation is a necessary consequence of the speed of light being constant in a vacuum, regardless of the speed of its source or its observer. This is what is meant by ‘deriving’ the equation. This derivation has always been a complicated piece of math reserved for advanced university courses in physics. It is, however, possible to derive the time dilation equation much more simply, so that an average ninth grade math student could understand it, if certain, apparently reasonable, assumptions are made about the universe we live in. So, let’s look at what these assumptions are, and go on to derive the equation in this magically simple way.
It is a basic fact about the universe, that we know indisputably, that electromagnetic energy is always moving at the speed of light compared to matter, regardless of how fast the matter is moving. It is equally true, however, to turn this around and say all matter is moving at the speed of light compared to all energy. All motion is relative. So all energy has a speed difference of the speed of light from all matter, or we could equally well say all matter has a speed difference of the speed of light from all energy. To make it easier to figure out what’s going on and make a model of how the universe might work, we can assume that one of these things, energy or matter, is always stationary (at rest) and the other is always moving at the speed of light. Since electromagnetic energy is always measured by us to be moving at the speed of light it would seem, at first sight, reasonable to assume all matter is stationary and all energy is moving at the speed of light, and this is basically what science has done until now. There are, however some problems with seeing it this way. For a start, matter is clearly not always stationary—different bits of matter are constantly moving with respect to each other, as soon as we get up and walk across the room, even if usually very slowly compared with the speed of light. What is more, on the grand scale of the cosmos, we know the universe is constantly expanding away from the big bang point, where the universe as we know it began, and that the speed of this expansion is about, and possibly even exactly, equal to the speed of light. That is one of the most amazing discoveries astronomers have made. Since we know all matter in the universe is moving away from the big bang point at about the speed of light, it would seem reasonable, then, to assume that all matter in the universe is moving at the speed of light, and all electromagnetic energy is stationary as measured from the big bang point.
But hold on, I hear you say, we see electromagnetic energy moving at the speed of light—it’s obvious that it’s doing the moving! How can you just turn the universe on its head and say EMR is stationary, and we are moving at the speed of light!—that’s absurd! Well, I would answer, it’s as you say, we see electromagnetic energy moving at the speed of light compared to us. But all motion is relative. We see the sun revolving around the Earth, rising in the east and traveling across the sky to the west, but we know nowadays that it is not actually the sun moving, but the Earth rotating that makes the sun appear to move across the sky. Likewise, if we were moving at the speed of light, and energy were stationary, it would appear to us that the energy was moving at the speed of light.
We have a universe that started out very small at the big bang, then expanded to get bigger, rather like a balloon being blown up.
In this analogy our universe is like the surface of the balloon, except it has an extra dimension. The surface of a balloon is two-dimensional, whereas in our universe space is the 'surface' and it is three-dimensional. On that balloon's 2-D surface you can go north, south, east or west, like on a map, but you can’t go up or down. If you were a two dimensional creature living on a balloon, however, you could figure out that there must be a third dimension in which your world curved around. One obvious way would be to walk right around your balloon and come back to the place you started. Although many people suspected the world was not flat, but a sphere, when some of Magellan’s crew sailed right around the world and back to where they started, they proved it beyond a shadow of a doubt. In a similar way (though not by traveling around it), we can infer that our universe has a fourth dimension in which it is curved around. The third dimension of the balloon creatures is at a right angle to each of the two dimensions they know (up and down are at right angles to both north-south and east-west). And this third dimension is the dimension in which the balloon is expanding, from its center out, though every point on the balloon surface is also moving away from every other point on their balloon, without any particular point being a stationary center.
Likewise with our universe, the fourth dimension, in which it is curved around, is at right angles to all three space dimensions. Like with the balloon surface world, every part of our three dimensional universe appears to be moving away from every other part, without any particular place being a stationary center, except that wherever you are seems like that stationary point. That means you could, if the universe were not expanding too fast to allow it, head off in any direction in space in a straight line, and eventually arrive back where you started, just like you could head of in any direction on the surface of a balloon and go round it and end up where you started. If the ‘sphere’ of the expanding universe were just in three dimensions, we would see it as sphere shaped, and be able to point to the direction in space where big bang point is, and see the universe arranged around it. We would be able to see the sphere from a point on its surface. All the nearby and medium distance galaxies would be just in one plane, and there would be no galaxies at all, except perhaps a few very close ones, in the direction away from the center of expansion. But what astronomers see instead is that there are very close to equal numbers of galaxies in every direction, all moving away from each other, with no center we can point to and no arrangement around any possible center point. And we don’t see a sphere. This means there must be an extra dimension, other than the three space dimensions we are aware of, in which our universe is curved around in. This dimension, at right angles to all three space dimensions, is the center-out direction in which our universe has been expanding from the big bang point. So, in our model of the universe, matter that seems to be stationary to us is actually moving through this extra dimension at the speed of light compared to the big bang point, while all the electromagnetic energy is stationary in all four dimensions compared to the big bang point.
If this model were correct, would we be able to sense, in any way, our movement through the fourth dimension at the speed of light? There is, in fact, one way in which we seem to move, even when we are stationary in space, and that is our constant movement through time. Could it be that what we are sensing as the passing of time is us moving through the fourth dimension at the speed of light? This would make the fourth dimension the time dimension, and indeed many scientists propose that there is a time dimension in order to make sense of how the universe is. They talk about us existing in ‘space-time.’
Let’s assume for a moment that these assumptions and the model of the universe they create are reasonable, and see what follows from them.
Since, under this model, we must always be traveling at the speed of light (like all matter), when we are stationary in space all this motion must be through the time dimension. But if we are traveling through space as well, our total speed must still be the speed of light, and if some of this speed is through space, then less of our speed would be though the time dimension, which means time would seem to slow down for us—which is what time dilation is. So, you can see, this model of the universe predicts time dilation. Under this model you don’t need complex math to show there should be time dilation, rather it is obvious that there must be time dilation for an object that has speed through space. But how much time dilation does this model say there should be? Let’s use some very simple math to work it out.
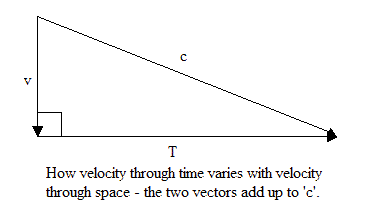
Since we have seen that the time dimension is at right angles to all three space dimensions, our velocity through time plus our velocity through space must add up to ‘c’, the speed of light, by a vector addition, where our velocity through time is at right angles to our velocity through space, which ever way we are going in space. The addition of the velocities is shown by this vector diagram:
Does this right-angled triangle look familiar? Can we use Pythagoras’s Theorem to see how our speed of travel through time, ‘T’, slows down as our speed of travel through space, ‘v’ increases? You bet we can! Since the square on the hypotenuse equals the sum of the squares on the other two sides, we can say:
c² = T² + v² or
T² + v² = c² (After all, if 3 = 2+1 then 2+1 = 3. It doesn’t matter which way round)
Now we subtract v² from each side of the equal sign to get:
T² = c² - v² (If you subtract the same amount from each side, it will still be equal.
If
Since we want to see how much time slows down compared with its normal value we want T0, to be on the right side of the equation, multiplied by whatever else. Since T0 is the speed of travel of time when there is no speed through space, or v = 0, you can see from the above vector diagram that when v = 0 then ‘T’ will be right next to ‘c’ and be exactly the same length, so T0 = c. As a result of this, getting the right side being something multiplied by ‘c’ would also have it being something multiplied by T0. We can do this by multiplying the term v² on the right by c²/c², which is the same as multiplying it by 1 (since any number divided by itself is 1), so it will not change its value, and the equation will still be true. Doing this, the equation becomes:
T² = c² - v²c²/c²
Taking the common factor of c² out of both terms on the right we get:
T² = c²(1 - v²/c²)
And taking the square root of each side, we get:
T = c(1 - v²/c²)½
(If two numbers are equal, their square roots will be equal, too. For
Example, 25 = 25 is true. If we take the square root of each side,
We get 5 = 5 which is also true.)
We figured out earlier that T0 = c, so we can now put T0 into the equation in place of 'c', as we want to do:
T = T0(1 - v²/c²)½
. . . . . (1)
This is an equation showing how much the speed of passing of time, ‘T’, slows down (gets smaller) as ‘v’ increases, where ‘c’ is, of course, the speed of light. It is already, as it is, an important equation that says a lot about the universe. It is one of the most important equations of the model of the universe we have been looking at.
As the speed of passing of time, ‘T’, decreases (gets smaller), the time each second lasts (its duration), which we call ‘t’, will increase (get larger). Scientists describe this relationship by saying these two quantities are inversely proportional to each other. This means that if one of them gets bigger, the other gets smaller by the same amount—for instance, if one gets twice as big the other shrinks to be half as big. We can express this in math by saying T = k/t (k divided by t), where k is a constant value that depends on what units we measure the duration of time in, seconds, minutes, or hours, for instance, but otherwise stays the same. To get an equation in terms of the duration of time, we can put k/t into equation 1, above, instead of T, and k/t0 instead of T0 to get:
k/t = (k/t0)(1 - v²/c²)½
The equation will still be equal if we divide both sides of it by the same amount, so we can divide each side by k (which just stands for some number) to get:
1/t = (1/t0)(1 - v²/c²)½
Finally, since both sides are equal, we can turn each side upside down and it will still be equal (for instance 2 = 2, and if we invert both sides we get ½ = ½, which is, of course still true). When we invert both sides of our equation, we get:
t = t0/(1 - v²/c²)½ . . . . . (2)
This is exactly the Lorentz transformation for a time interval, the time dilation equation of Einstein’s Special Relativity, that we looked at earlier, and used to show how time travel into the future is possible. As we said earlier, it is normally rather difficult to derive this equation, but we have derived it just by using Pythagoras’s theorem and changing each side of the equation in the same ways to keep it equal until we got what the duration of a time interval ‘t’ equaled.
Everyone has heard of this famous equation of Einstein’s that tells us how much energy, ‘E’, is produced when matter with a mass of ‘m’ is converted to electromagnetic radiation in nuclear reactions such as happen in atomic bombs and in the sun. It is a huge amount of energy, because the speed of light, ‘c’, is a very large number and ‘c²’ is astronomically huge. Can the model of the universe we used to derive the time dilation equation also be used to derive E = mc²? Yes, indeed it can, and very simply. Here’s how:
According to our model, all matter is traveling at the speed of light, very largely through the time dimension, as our universe expands from the big bang point, and electromagnetic energy is stationary compared to the big bang point. This model also assumes that matter and electromagnetic energy are two states of the same thing, since it is known they can be converted to each other, and that the only difference is their speed—energy being stationary and matter traveling at the speed of light. The energy due to the motion of an object is called kinetic energy, and the equation for kinetic energy is:
E = ½mv²
where ‘m’ is the object’s mass and ‘v’ is its velocity. (This equation for kinetic energy is quite simple to derive, and many websites show the derivation if you are interested.) Since, under this model, all matter is traveling at the speed of light, ‘c’, compared to the big bang point, the kinetic energy a piece of matter has in this frame of reference is:
E = ½mc²
If this piece of matter were slowed down to zero speed to become electromagnetic radiation (EMR), this amount of energy would be released. But how could a particle of matter flying through space-time at the speed of light be stopped to become EMR? Newton’s first law of motion says:
This means that to stop a particle like this there must be an external force—it cannot stop itself. But what could this external force be? The only obvious thing that could stop a fast moving particle in its tracks like that would be if it collided with a particle of the same mass going the opposite direction at the same speed, like two cars in a head-on collision. Let’s assume for a moment that this is what happens—that matter converts to energy when a particle of matter going forward through time at the speed of light collides with a particle of the same mass going backward through time at the speed of light. We would only be aware of the forward through time particle, as that is the domain we live in, except when these collisions happen. And when these collisions happen the kinetic energy from both these particles will be released, which in terms of the mass we are aware of, ‘m’, is:
E = ½mc² + ½mc²
And adding the two terms on the right together, we get:
E = mc² . . . . . (3)
And there we have it! The most famous equation in all of science, derived simply by adding together the kinetic energies of two colliding particles, each of the same mass and traveling at the speed of light in opposite directions.
Does being able to simply derive the time dilation equation and E = mc² from it mean the model of the universe presented in this article is true? No…it doesn’t mean it is true, but it does mean it could be true, and could be looked into further. In the scientific method, no theory can ever be proved to be true, it can only be proved to be false if an experiment or observation shows it to be wrong. Scientific theories do gain credence, though, and become useful, if they don’t get disproved and can make predictions that turn out to be true.
The model of the universe I’ve presented here is based on the speed of light always being measured as being the same, the speed of light in a vacuum, ‘c’. But in fact light is measured as slowing down slightly when it passes through a transparent medium like glass. This slowing down refracts light, enabling lenses to work to focus light. Since this model says light always travels at the speed ‘c’, this model predicts that light in fact travels at the speed ‘c’ in transparent media when it is moving, but is absorbed by molecules and re-emitted at the same frequency and in close to the same direction, and since it spends a small amount of time stopped, its average speed will be measured to be slightly lower than ‘c’. It has already been determined that in certain media where light or other EMR is slowed down a lot, that it is because the medium is absorbing it and re-emitting it a little later. This model, though, predicts this absorbing and re-emitting of light and other EMR happens in all transparent media in which the speed of EMR seems to slow down. If future experiments show this is true, it will support this model; if it shows it is not true, then the model will be disproved. This model also makes various other predictions, such as that scientists will not be able detect large amounts of dark energy or non-neutrino, non-baryonic dark matter—because they don’t need to exist when the universe is viewed through the frame of this model. Up to this point, scientists have not been able to detect any of this dark energy or dark matter.
This is some of the magical math of the universe, and it certainly seems to suggest God loves simple math, though some of His geometry may, at times, be a little complicated and difficult to visualize.
If you wish to find out more about this model of the universe, you can read an introductory article about it by clicking here.
Copyright © 2016 Mark Mason
If you have questions or comments: To go to the Home Page of this website, please click here.
To return to the Top of This Page, please click here.
Likewise, c² = 9 x 1016
So v²/c² = (8.8209/9) x (1016/1016) = 0.9801 x 1 = 0.9801
So 1 - v²/c² = 1 – 0.9801 = 0.0199
Now press the '√' button to get: (1 - v²/c²)½ = 0.141067
Finally, since t0 = 1, press the 1/x button to get:
t0/(1 - v²/c²)½ = 1/0.141067 = 7.1
Deriving the Time Dilation Equation
The Apparently Reasonable Assumptions

Deriving the Time Dilation Equation
we start with 5 = 5 then subtract two from each side we get 3 = 3)
Deriving E = mc²
Every object will remain at rest or in uniform motion in a straight line unless compelled to change its state by the action of an external force.
The Scientific Method
Conclusion
