Article 22:
How the Gravitational Red Shift Can Power the Fast Solar Wind

This is a supplementary article. To go to the main introductory article about Stationary Energy Theory, and its links to other supplementary articles, please click here.

I am going to show you how the energy lost from the gravitational red shift of light coming from the photosphere of the sun is sufficient to power all of the fast solar wind. The mechanism for how this would happen is a prediction of a new theory of cosmology and gravity that I have developed, which also correctly predicts the speeds of the solar wind, its composition, and the ratio of matter lost through the solar wind to the matter converted to energy in fusion reactions. You can read about this overall theory by clicking here. Meanwhile, I will show you the math pertaining these aspects of the gravitational red shift powering the solar wind.

Since the red shift at the surface of the Sun is Z = 2.12239 x 10^-6, and energy is proportional to frequency, then the total energy lost in the gravitational red shift when a particle of mass m, such as a proton is converted to energy is: E = Z x mc². For reasons dictated by my new gravitational theory, only half this energy loss can be converted to kinetic energy in a particle of the solar wind. So we get KE = Z x ½mc². The speed of this solar wind particle will be much lower than the speed of light, of course, because Z is such a small number. Its speed can be calculated by equating the energies:

½m_wv² = Z x ½m_cc²

where m_w is the mass of the solar wind particle, and m_c is the mass of the particle(s) being converted to EMR by fusion reactions. So,

v² = Zc²m_c/m_w
or
v = cZ^½(m_c/m_w)^½            .           .           .           .            .            (17)

For our sun, using velocities in km/sec:
v = 299792 x 0.001456842476 x (m_c/m_w)^½
or
v = 436.74972 x (m_c/m_w)^½            .           .           .           .           (17.1)

In the case where one proton is converted into energy, and the red-shift energy loss is carried away as one proton in the solar wind, (m_c/m_w)^½ = 1 and v = 437 km/s.

In the case where two protons are converted to energy, and the red-shift energy loss is carried away as one proton in the solar wind, v = 436.74972 x 2^½ = 618 km/s.

In the case where three protons are converted to energy, and the red-shift energy loss is carried away as one proton in the solar wind, v = 436.74972 x 3^½ = 756 km/s.

In the case where four protons are converted to energy, and the red-shift energy loss is carried away as one proton in the solar wind, v = 436.74972 x 4^½ = 873 km/s.

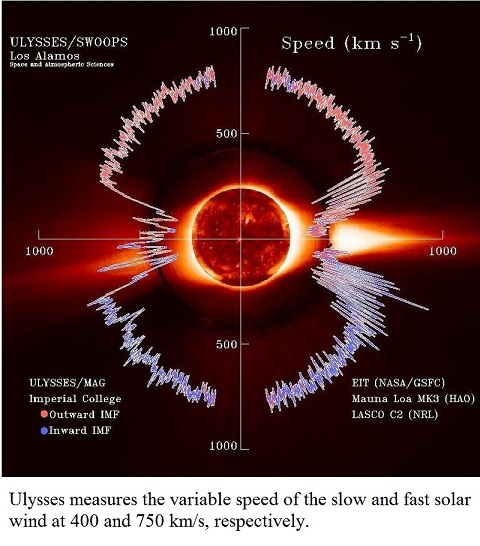
One would expect the measured speeds of solar wind particles to vary somewhat from these speeds due to gravitational slowing and magnetic field acceleration. Overall, though, these speeds correspond well to the speeds of the solar wind observed by the Ullyses space craft, as shown in the diagram below. The one particle conversion solar wind speed of 437 km/s is typical of the speed of the slow solar wind, which you can see from the diagram varies from just below 400 km/s to almost 500 km /sec. The two particle conversion solar wind speed of 618 km/s is significant, as this is also the escape velocity of the sun, so it represents the lower speed limit of the fast solar wind. The three and four particle conversion solar wind speeds of 756 km/sec and 873 km/s are typical of the speeds of the fast solar wind. And the average of the two, three and four particle conversion solar wind speeds of 749 km/s is right on the fast solar wind average of 750 km/s. As you can see, this theory explains why the solar wind speeds are grouped into specific ranges, rather than spreading across a continuous spectrum of speeds. This theory predicts that the speed of the stellar winds of other stars, should they ever come to be measurable, will be able to be calculated from the above formulas, as we have done for our sun.

These figures, above, would suggest that an average of about one part of matter is lost to the sun due to the fast solar wind for each three parts of matter converted to solar energy by the fusion process, as the average fast solar wind speed of 750 km/s corresponds with one particle of matter carrying away kinetic energy as solar wind for each three particles being converted to energy. This is in line with the figures astronomers give us for the rate of conversion of solar matter to energy of 4.26 x 10⁹ kg/s and the loss of matter from the sun due to solar wind of 1.3 x 10⁹ kg/s to 1.9 x 10⁹ kg/s. This is a ratio of between 1 to 2.2 and 1 to 3.3, right in line with the approximate 1 to 3 ratio this theory predicts.

One of the problems we have had up to now with our theories about solar wind is that it is not understood how the fast solar wind can accelerate up to the speeds it does. As we can see from the above calculations, though, the carrying away of excess energy from the gravitational red shift of the sun (even though the red shift itself is too small to be easily observed), could certainly account for the levels of kinetic energy of the fast solar wind. Stars with much higher gravitational fields than our sun (which are much more massive and/or denser), could also, in the same way, produce Cosmic Rays, which, like the solar wind, are mostly protons and electrons, but are much faster than the solar wind, nudging the speed of light.

Is there enough energy lost from the sun’s gravitational red shift to produce the solar wind?

With this rate of conversion of matter to enegry, the amount of energy lost by the sun’s gravitational red shift, measured by its mass, is:

Energy lost = Z_s x 4.26 x 10⁹ kg/s = 2.12239 x 10^-6 x 4.26 x 10⁹ kg/s = 9.04 x 10³ kg/s

This 9.04 x 10³ kg/s is the amount of matter that would carry away half the lost energy as KE if it were traveling at the speed of light, “c” (the other half is carried off in another domain that the theory describes). This amount of KE could also be carried away by about 160,000 (close to 1/(3Z)) times as much matter if its speed were 750 km/s, a typical speed for the fast solar wind. This would give a total possible rate of emission of fast solar wind (SWf) of:

SWf = 9.04 x 10³ x 160,000 kg/s = 9.03 x 10³ x 1.6 x 10⁵ kg/s = 1.45 x 10⁹ kg/s

This rate of emission of 1.45 x 10⁹ kg/s is right in the range of the estimated loss of matter from the sun due to the solar wind, which is about 1.3 x 10⁹ kg/s to 1.9 x 10⁹ kg/s. This is based on the assumption that the solar wind starts at the photosphere at a speed of 750 km/s. If the fast solar wind starts off at a much higher speed and is slowed down the sun's gravity more than it is sped up by magnetic fields, then this mechanism might only cause the fast solar wind, and not also the slow. There are, of course, other mechanisms that can explain the slow solar wind. It is clear, though, from the above calculations, that all of the fast solar wind, at least, can be produced by energy lost from the sun’s gravitational red shift. This gravitational red shift explanation of the production of the fast solar wind has the particles of the fast solar wind originating at the photosphere. As a result, one would expect, from this theory, that the elemental composition of the the fast solar wind should resemble that of the photosphere. It is interesting to note that observational data indeed shows this to be the case. The fact that the slow solar wind has a different elemental composition suggests that it is not all produced by this gravitational red shift mechanism.

The author can be contacted by email as follows:

Again, to go to the article describing the cosmology and gravity theory these calculations are derived from, please click here.

Copyright © 2011-2016, Mark J. Mason