Article 21:
Possible Parallel Universes in Stationary Energy Theory

This is a supplementary article. To go to the main introductory article about Stationary Energy Theory, and its links to other supplementary articles, please click here.

Stationary Energy Theory is neutral about whether there are multiple parallel physical universes in our cosmos, or whether there is just the one we occupy. This theory can, however, accommodate many extra physical universes. In terms of the "inflating balloon" model of the universe (see diagram below), where the surface of the balloon represents our three dimensional physical universe expanding through the old energy blueprint of the universal energy field, it would mean there would be many "balloons" within the energy field. If these balloons were spaced apart from each other, eventually, as they expanded, they would run into each other, which would probably not be good! Fortunately, there is one possible arrangement where this doesn't happen: a slightly less inflated balloon inflating inside a more inflated balloon, and a still less inflated one inflating inside that, and so on, each having the same center. We could call them "concentric parallel universes." If they were each inflating at the same rate they would never run into each other, just expand together, rather like the layers of a growing onion bulb. This model has elegance to recommend it, and it is the one we will look at.

A cross section of the balloon model of the universe is just a circle, where the circle represents our physical universe at a given time, such as the present. It is an expanding circle, of course, so would have had a smaller radius in the past, and will have greater one in the future. The following diagram shows this circle model:

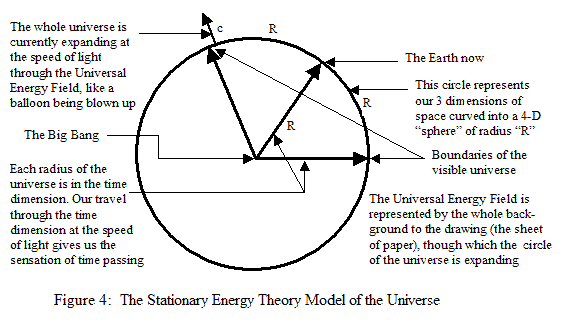
In terms of this circle model, a cosmos with concentric parallel universes would look like the following diagram, though there would probably be many more physical universes that the eight shown:

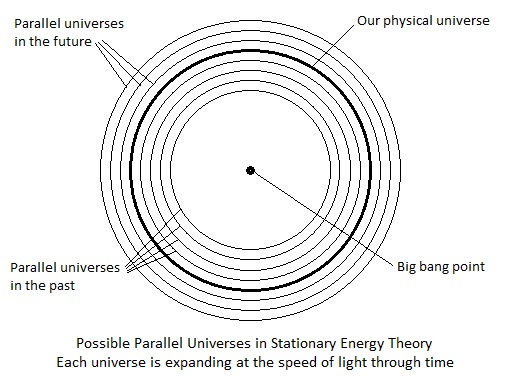
Note that on the diagram the parallel universes outside our universe are labelled "parallel universes in the future" and the ones inside our own are labelled "parallel universes in the past." This is because our universe, and the other parallel universes are expanding at the speed of light through the time dimension, and the universes outside our own have expanded further than we have and have already passed though our point in time. Likewise, the universe inside ours are yet to reach the position in time that we have reached, so the part of the energy blueprint they are scanning is a part we already have scanned at some point in our past. We could say the parallel universes are stacked chronologically.

Since each of the past universes is scanning the same cosmic blueprint that we have already scanned in the past, and this blueprint specifies how the organized complexity of the material universe unfolds, are these universes identical to what ours was when we passed through that point in time? And are the future universes identical to what ours will be when we reach their time? The answer is probably that at the same point in time each of the universes is very similar to the others, but will differ in significant ways. Let me explain why.

If we lived in a completely deterministic cosmos, where sentient beings like us had no free will at all, then all the universes would be identical. But since we do have free will, and can make choices, the old energy cosmic blueprint, as we have discussed in the main article, must be able to reprogram itself to take our free-will decisions into account, and the sentient beings in other parallel universes, though they might look much like us, and be versions of ourselves, have the free will to make different choices from what we have made. Many of the choices they make may well be the same as our choices, but some will be different, making the other parallel universes somewhat different from our own.

Can we ever experience these other parallel universes? I don't know, of course, but there are some clues that we might be able to. J. W. Dunne's book An Experiment with Time tells the story of an experiment showing that we can and do dream of the future as well as the past. If ours were the only universe, there would be no physical reality in the future yet to see - only the old energy blueprint. So either our dreams are constructing a version of the future from the old energy blueprint, or there are future parallel universes, and we are able to see them. When psychics "see" the future, the best of them, who are "seeing" something, are uncannily accurate in many details but often totally wrong in others. This would be consistent with them "seeing" a future parallel universe, as that universe would be very similar to what ours will turn out to be, but could differ in significant details due to different free-will decisions being made by their inhabitants. So such psychics are seeing possibilities, not fixed-in-stone inevitabilities.

Likewise, people sometimes have memories of the past that differ from what most people remember. An example of this is the so-called Mandela Effect, in which a lot of people, but still a tiny minority, "remember" that Nelson Mandela died in prison during the 1980s, and never lived to be president of South Africa. These people are not saying their memory is right and the memory of the vast majority is wrong, they are just saying what they remember. Some of them have even suggested that what they experienced was a "bleed through from a parallel universe." What could have happened is that they experienced a past parallel universe, in a dream, where Nelson Mandela actually did die in prison, and remembered the dream. This would explain the memory, and also how it was that many people had the same memory - there was actually an objective reality out there, in a parallel universe, that they all experienced, where Nelson Mandela died in prison.

Perhaps research will cast more light on this subject in the future. Meanwhile, the point is that Stationary Energy Theory can accommodate the possibility of parallel universes, not that it predicts or requires them.

One last thought. If there are multiple concentric parallel universes out there, as considered here, each of the many universes must have had its own "big bang" to start it off, but these big bangs would all have taken place at the same point in space-time. The big bang point would have been like a cannon, firing off multiple rounds, each one exploding to become a universe with its own timeline. The ultimate fireworks show!

Mark Mason
5/30/2018

The author can be contacted by email as follows:

Again, to go to the article describing the cosmology and gravity theory this article is based on, please click here.

Copyright © 2011-2018, Mark J. Mason